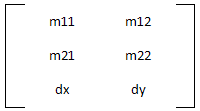Sous GDI+, les objets Matrix sont des matrices que l'on peut se représenter sous la forme d'un tableau ayant trois lignes et trois colonnes.
Ces matrices permettent d'appliquer
des transformations géométriques.
Les matrices de 3 ×3 peuvent représenter une transformation affine. Un objet
Matrix stocke seulement six des 9 nombres d'une matrice 3 ×3 parce
que toutes les matrices de 3×3 qui représentent des transformations affines
ont la troisième colonne identique (0, 0, 1).
GDI+ défini plusieurs types de matrices qui utilisent des nombres entiers ou des nombres flottants, il est possible de définir les six éléments de la matrice individuellement ou de la définir à partir d'une combinaison rectangle/points.
Les matrices GDI+ se représentent sous la forme 3 lignes et 2 colonnes. Il y a six points définissables représentant les trois transformations suivantes :
La mise à l'échelle (scale)
La rotation (rotate)
La translation (translate.)
Représentation de la matrice.
m11
Valeur de l'élément à l'intersection de la première ligne et de la première colonne.
Ce paramètre représente le facteur de mise à l'échelle selon l'axe X (scale).
m12
Valeur de l'élément à l'intersection de la première ligne et de la deuxième colonne.
Ce paramètre représente le facteur de rotation, coordonnée X (rotate).
m21
Valeur de l'élément à l'intersection de la deuxième ligne et de la première colonne.
Ce paramètre représente le facteur de rotation, coordonnée Y (rotate).
m22
Valeur de l'élément à l'intersection de la deuxième ligne et de la deuxième colonne.
Ce paramètre représente le facteur de mise à l'échelle selon l'axe Y (scale).
dx
Valeur de l'élément à l'intersection de la troisième ligne et de la première colonne.
Ce paramètre représente la translation selon l'axe X (translate).
dy
Valeur de l'élément à l'intersection de la troisième ligne et de la deuxième colonne.
Ce paramètre représente la translation selon l'axe Y (translate).
Les 4 éléments m11, m12, m21, m22 sont liés par une relation trigonométrique. Voir les explications ici GdipCreateMatrix2()
Le concept GDI+ est spécifiquement orienté objet. De ce fait, les matrices possèdent des méthodes et des propriétés.
Les méthodes se chargeront
du calcul matriciel (multiplication, inversion, translation, rotation etc.).
Les propriétés permettent de retrouver les éléments
des matrices.
La fonction GdipSetImageAttributesColorMatrix() utilise une matrice de 5x5 défini à partir d'une variable basée sur la structure ColorMatrix.
Les transformations géométriques
:
Il est possible d'effectuer la transformation géométrique sur
un objet et de nombreux objets possèdent des fonctions de transformations
simples qui ne s'appliquent qu'à eux-même.
La transformation est dite locale lorsqu'elle
n'affecte qu'un objet en particulier, par exemple une brush, un texte, une
image etc. L'effet n'est pas appliqué au graphique complet.
La transformation est dite globale lorsqu'elle
affecte le graphique et tous les objets qu'il contient.
La transformation est dite composite
lorsqu'il s'agit de plusieurs transformations globales enchaînées.
Valeur de retour:
D'une manière générale, les fonctions retournent les valeurs suivantes :
Si la fonction réussit, elle retourne #Ok qui est une constante de l'énumération status.
Si la fonction échoue, elle retourne une des autres valeurs de l'énumération status.
Sous PureBasic, nous utiliserons
la programmation classique par l'appel direct des fonctions GDI+.
Page d'explications sur les matrices de Microsoft.
http://windowssdk.msdn.microsoft.com/en-us/library/ms536397.aspx