Un objet ImageAttributes conserve les paramètres de réglage des couleurs et des nuances de gris pour cinq catégories de réglages : par défaut, bitmap, brush, pen et text.

Les paramètres de réglage des couleurs et des nuances de gris par défaut s'appliquent à toutes les catégories qui n'ont pas de paramètres de réglage propres. Par exemple, si vous ne spécifiez jamais de paramètres de réglage pour la catégorie pen, les paramètres par défaut s'appliquent à cette catégorie. Dès que vous spécifiez un paramètre de réglage des couleurs ou des nuances de gris pour une catégorie donnée, les paramètres de réglage par défaut ne s'appliquent plus à cette catégorie. Par exemple, supposons que vous spécifiez un ensemble de paramètres de réglage pour la catégorie par défaut. Si vous définissez le seuil (plage de transparence) de la catégorie pen en passant #ColorAdjustTypePen à la fonction GdipSetImageAttributesThreshold(), aucun des paramètres de réglage par défaut ne s'appliquera aux pen.
Vous pouvez rétablir les réglages par défaut pour cette catégorie en utilisant la fonction GdipResetImageAttributes().

Lorsque le paramètre flags vaut #ColorMatrixFlagsDefault toutes les couleurs (y compris les gris) sont réglées par la matrice de réglage des couleurs (colorMatrix.ColorMatrix) et non par la matrice de réglage des nuances de gris (grayMatrix.ColorMatrix). Par conséquent, la matrice de réglage des nuances de gris passée à cette fonction n'a aucun effet.

L'utilisation d'une matrice 5x5 va permettre d'effectuer les transformations suivantes sur les couleurs :

Translation (translation)
La mise à l'échelle (scaling)
Rotation (rotation)
Inclinaison (Shearing)

Voir les explications de Microsoft ici :
   http://msdn2.microsoft.com/en-us/library/ms533809.aspx

Par convention, les éléments des matrices 5x5 ont 5 lignes et 5 colonnes dont les indices commencent à 0. Par exemple l'élément de la cinquième ligne et de la troisième colonne est notée M[4][2]
Voici la représentation d'une matrice 5x5 (25 éléments) avec la numérotation de chaque élément :

Les matrices 5x5 (GDI+) ont toujours l'élément au croisement de la cinquième ligne et cinquième colonne (M[4][14] (noté M44 sur la représentation) à 1 et tous les autres éléments de la cinquième colonne à 0.

On pourra appliquer une ou plusieurs des transformation précédentes en un seul appel de la fonction. Il suffit de modifier les paramètres de la matrice en consquence avant d'appeler la fonction.

GDI+ utilise la convention qui définit la représentation des composantes des couleurs avec la valeur 1 (100%) pour le maximum d'intensité et le nombre 0 pour le minimum d'intensité (0%) pour les transformations de couleurs. Une couleur possède les composantes rouge, verte, bleue et alpha (transparence) et les transformations utilisent des vecteurs de couleurs. Les quatre premiers composants du vecteur de couleurs sont et dans cet ordre le rouge, le vert, le bleu et la couche alpha (transparence). Le cinquième composant du vecteur est toujours à 1.

Par ce biais on peut écrire la couleur ayant le rouge à $66, le vert à $00, le bleu à $33 et la transparence à $FF comme ceci :
   le rouge à $66 représente 40% de l'intensité maximale (qui vaut $FF (255))
   le vert à $00 représente 0% de l'intensité maximale (qui vaut $FF (255))
   le bleu à $33 représente 20% de l'intensité maximale (qui vaut $FF (255))
   la couche alpha à $FF représente 100% de l'intensité maximale (qui vaut $FF (255))

  La couleur peut s'écrire : (0.4, 0, 0.2, 1)

La Translation des couleurs :

Documentation MS ici :    http://msdn2.microsoft.com/en-us/library/ms533873.aspx

La translation de couleur ajoute une valeur à une ou plusieurs des quatre composantes de la couleur. Les entrées de la matrice des couleurs qui représentent les translations sont données dans la table suivante :

Composante pour la translation	Entrée de la matrice
Rouge/Red	[4][0]
Vert/Green	[4][1]
Bleu/Blue	[4][2]
Alpha	[4][3]

Exemple : On charge une image avec quatre barres verticales de couleurs différentes (voir image). on applique une translation de 0,6 à la composante rouge de chaque pixel de l'image. L'entrée de la matrice M[4][0] aura la valeur 0.6 et les entrées M[0][0],M[1][1], M[2][2], M[3][3] seront à 1 car elles correspondent à la mise à l'échelle des 4 composantes et n'entraîne pas de modification (voir ci-dessous la mise à l'échelle). L'entrée M[4][4] est toujours à 1.

Le résultat de l'addition est plafonnée à 1.00, c'est-à-dire que si par exemple on a 0.5 + 0.7 = 1.2, GDI+ utilisera la valeur maxi de 1.00 pour la translation.

En notation PureBasic, on pourra créer cette matrice comme ceci (variable M.ColorMatrix).

; Matrice de transformation, ajoute 0.6 à la composante rouge de chaque pixel de l'image source Matrix\M00 = 1.0 : Matrix\M01 = 0.0 : Matrix\M02 = 0.0 : Matrix\M03 = 0.0 : Matrix\M04 = 0.0 Matrix\M10 = 0.0 : Matrix\M11 = 1.0 : Matrix\M12 = 0.0 : Matrix\M13 = 0.0 : Matrix\M14 = 0.0 Matrix\M20 = 0.0 : Matrix\M21 = 0.0 : Matrix\M22 = 1.0 : Matrix\M23 = 0.0 : Matrix\M24 = 0.0 Matrix\M30 = 0.0 : Matrix\M31 = 0.0 : Matrix\M32 = 0.0 : Matrix\M33 = 1.0 : Matrix\M34 = 0.0 Matrix\M40 = 0.6 : Matrix\M41 = 0.0 : Matrix\M42 = 0.0 : Matrix\M43 = 0.0 : Matrix\M44 = 1.0

Résultat de la translation :

Image d'origine	Image après translation

 

La mise à l'échelle (scaling) des couleurs :

Documentation MS ici :    http://msdn2.microsoft.com/en-us/library/ms533869.aspx

La mise à l'échelle de couleur multiplie une ou plusieurs des quatres composantes de la couleur par une valeur. Les entrées de la matrice des couleurs qui représentent la mise à l'échelle sont données dans la table suivante :

Composante pour la mise à l'échelle	Entrée de la matrice
Rouge/Red	[0][0]
Vert/Green	[1][1]
Bleu/Blue	[2][2]
Alpha	[3][3]

Exemple : On charge une image avec quatre barres verticales de couleurs différentes (voir image). La mise à l'échelle est la suivante pour chaque pixel de l'image : La composante rouge est réduite de 25 pour cent, la composante verte est réduite de 35 pour cent et la composante bleue est réduite de 50 pour cent et la couche alpha est inchangé. L'entrée de la matrice M[0][0] aura la valeur 0.75, l'entrée M[1][1] aura la valeur 0.65, M[2][2] aura la valeur 0.50, M[3][3] aura la valeur 1.00. L'entrée M[4][4] est toujours à 1.

Il est possible d'avoir les entrées de la mise à l'échelle supérieure à 1. Par exemple, si une composante est à 0.6 et que l'on applique une mise à l'échelle de 200% (l'entrée correspondante de la matrice vaudra 2.0) on obtiendrait 2 x 0.6 soit 1.2. GDI+ dans le cas de la mise à l'échelle ne retient que la partie après la virgule, 0.2 pour cet exemple.

En notation PureBasic, on pourra créer cette matrice comme ceci (variable M.ColorMatrix).

; Matrice de mise à l'échelle : rouge x 0.75, vert x 0,65 et bleu x 0,50 Matrix\M00 = 0.75 : Matrix\M01 = 0.00 : Matrix\M02 = 0.00 : Matrix\M03 = 0.0 : Matrix\M04 = 0.0 Matrix\M10 = 0.00 : Matrix\M11 = 0.65 : Matrix\M12 = 0.00 : Matrix\M13 = 0.0 : Matrix\M14 = 0.0 Matrix\M20 = 0.00 : Matrix\M21 = 0.00 : Matrix\M22 = 0.50 : Matrix\M23 = 0.0 : Matrix\M24 = 0.0 Matrix\M30 = 0.00 : Matrix\M31 = 0.00 : Matrix\M32 = 0.00 : Matrix\M33 = 1.0 : Matrix\M34 = 0.0 Matrix\M40 = 0.00 : Matrix\M41 = 0.00 : Matrix\M42 = 0.00 : Matrix\M43 = 0.0 : Matrix\M44 = 1.0

Résultat de la mise à l'échelle :

Image d'origine	Image après mise à l'échelle

La rotation (rotating) des couleurs :

Documentation MS ici :    http://msdn2.microsoft.com/en-us/library/ms533866.aspx

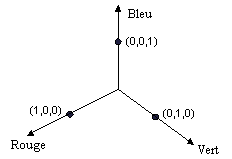
Il est difficile de visualiser la rotation dans un espace de couleurs à quatre dimensions. Si nous gardons une des composantes de couleurs fixe, la rotation sera plus facile à voir. Par exemple, si on conserve la composante alpha à 1 (opacité complète, alors on peut visualiser un espace de couleur tridimensionnel avec les axes rouges, verts et bleus comme l'illustre la figure suivante.

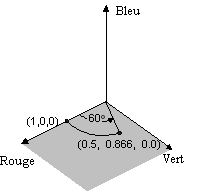
Une couleur peut être considérée comme un point dans un espace 3D. Par exemple, le point (1, 0, 0) dans l'espace représente la couleur rouge et le point (0, 1, 0) dans l'espace représente la couleur verte. La figure suivante montre ce que signifie la rotation de la couleur (1, 0, 0) d'un angle de 60 degrés dans le plan Rouge-Vert. La rotation dans un plan parallèle au plan Rouge-Vert peut être considérée comme la rotation autour de l'axe bleu.

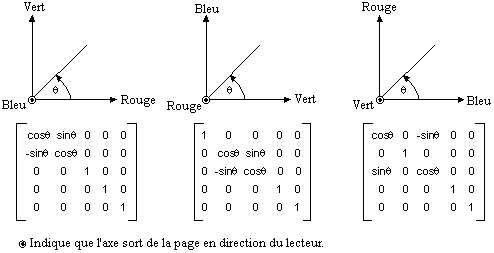
La figure suivante montre comment initialiser une matrice de couleurs pour exécuter des rotations de chacun des trois axes (rouge, vert, bleu).

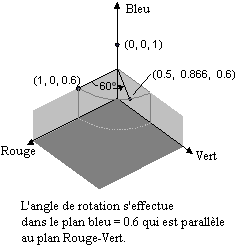
Exemple : L'exemple utilise une image qui a une couleur unie (1, 0, 0.6) et applique une rotation de 60 degrés autour de l'axe bleu. L'angle de la rotation suit un plan qui est parallèle au plan Rouge-Vert. L'angle doit être converti en radian pour la matrice.

En notation PureBasic, on pourra créer cette matrice comme ceci (variable M.ColorMatrix).

r = 60 * #PI / 180 Matrix\M00 = Cos(r) : Matrix\M01 = Sin(r) : Matrix\M02 = 0.00 : Matrix\M03 = 0.0 : Matrix\M04 = 0.0 Matrix\M10 = -Sin(r) : Matrix\M11 = Cos(r) : Matrix\M12 = 0.00 : Matrix\M13 = 0.0 : Matrix\M14 = 0.0 Matrix\M20 = 0.00 : Matrix\M21 = 0.00 : Matrix\M22 = 1.00 : Matrix\M23 = 0.0 : Matrix\M24 = 0.0 Matrix\M30 = 0.00 : Matrix\M31 = 0.00 : Matrix\M32 = 0.00 : Matrix\M33 = 1.0 : Matrix\M34 = 0.0 Matrix\M40 = 0.00 : Matrix\M41 = 0.00 : Matrix\M42 = 0.00 : Matrix\M43 = 0.0 : Matrix\M44 = 1.0

Résultat de la rotation (60° autour de l'axe bleu):

Image d'origine	Image après rotation

La rotation de le couleur effectuée dans l'exemple précédent peut être visualisée comme ceci :

L'inclinaison (Shearing) des couleurs :

Documentation MS ici :    http://msdn2.microsoft.com/en-us/library/ms533871.aspx

L'inclinaison augmente ou diminue une composante de couleur par un montant proportionnel à une autre composante de couleur. Par exemple, la composante rouge pourrait être augmentée de la moitié de la valeur de la composante bleue. Avec une transformation de ce style, la couleur (0.2, 0.5, 1) deviendrait (0.7, 0.5, 1). La nouvelle composante rouge devient : 0.2 + (1/2)(1) = 0.7

Les entrées de la matrice des couleurs l'inclinaison sont données dans la table suivante avec en en-tête de colonne la couleur à laquelle sera ajoutée un pourcentage d'une autre couleur, la référence de cette autre couleur est au début des lignes :

	Rouge/Red	Vert/Green	Bleu/Blue	Alpha
Entrée de la matrice pour l'ajout du rouge	---	[0][1]	[0][2]	[0][3]
Entrée de la matrice pour l'ajout du vert	[1][0]	---	[1][2]	[1][3]
Entrée de la matrice pour l'ajout du bleu	[2][0]	[2][1]	---	[2][3]
Entrée de la matrice pour l'ajout de l'alpha	[3][0]	[3][1]	[3][2]	---

A noter par exemple que si l'on ajoute un pourcentage de rouge au rouge, cela revient à faire une mise à l'échelle de la composante rouge.

Exemple : On charge une image avec quatre barres verticales de couleurs différentes (voir image). L'inclinaison est la suivante pour chaque pixel de l'image : On ajoute à la composante rouge une valeur qui est de la moitié (50%) de la valeur de la composante bleue. Les autres composantes restent inchangées, L'entrée de la matrice M[2][0] aura la valeur 0.50 qui représente 50% de la valeur de la composante bleue ajouté au rouge. Les entrées M[0][0],M[1][1], M[2][2], M[3][3] seront à 1 car elles correspondent à la mise à l'échelle des 4 composantes et n'entraîne pas de modification (voir la mise à l'échelle). L'entrée M[4][4] est toujours à 1.

En notation PureBasic, on pourra créer cette matrice comme ceci (variable M.ColorMatrix).

; Matrice d'inclinaison des couleurs, rouge + 50% du bleu Matrix\M00 = 1.00 : Matrix\M01 = 0.0 : Matrix\M02 = 0.0 : Matrix\M03 = 0.0 : Matrix\M04 = 0.0 Matrix\M10 = 0.0 : Matrix\M11 = 1.00 : Matrix\M12 = 0.0 : Matrix\M13 = 0.0 : Matrix\M14 = 0.0 Matrix\M20 = 0.5 : Matrix\M21 = 0.0 : Matrix\M22 = 1.00 : Matrix\M23 = 0.0 : Matrix\M24 = 0.0 Matrix\M30 = 0.0 : Matrix\M31 = 0.0 : Matrix\M32 = 0.0 : Matrix\M33 = 1.00 : Matrix\M34 = 0.0 Matrix\M40 = 0.0 : Matrix\M41 = 0.0 : Matrix\M42 = 0.0 : Matrix\M43 = 0.0 : Matrix\M44 = 1.00

Résultat de l'inclinaison :

Image d'origine	Image inclinaison

L'exemple du fichier reprend tous ces exemples en affichant à gauche les images originales et à droites les images ayant subies une transformation des couleurs.