Cette matrice permet de définir les trois transformations suivantes (transformation composite):
La mise à l'échelle (scale)
La rotation (rotate)
La translation (translate)
Selon les valeurs des paramètres, il est possible d'utiliser une, deux ou trois transformations.
Représentation de la matrice.
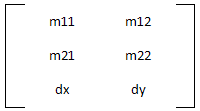
Il existe une relation trigonométrique entre les éléments de la mise à l'échelle (m11, m22) et les éléments de la rotation (m12, m21).
Prenons un exemple :
on appelle a le facteur voulu de mise à l'échelle selon l'axe X
on appelle b le facteur voulu de mise à l'échelle selon l'axe Y
on appelle alpha l'angle de rotation voulu en degré
Les relations entre m11, m22, m12 et m21 sont les suivantes :
m11 = a.cos(alpha)m12 =b.sin(alpha)
m21 = a.(-sin(alpha))
m22 = b.cos(alpha)
Exemple numérique :
a = 4 (mise à l'échelle selon l'axe X de 4)
b = 2 (mise à l'échelle selon l'axe Y de 2)
alpha = 30 degrésm11 = a.cos(alpha) = 4.cos(30) = 3,464101
m12 =b.sin(alpha) = 2.sin(30) = 1
m21 = a.(-sin(alpha)) = 4.(-sin(30)) = -2
m22 = b.cos(alpha) 2.cos(30) = 1,732050En prenant une translation nulle en X et Y on aura le code suivant :
GdipCreateMatrix2(3.464101, 1, -2, 1.732050, 0, 0, @*matrix)Cas particulier :
a = 4 (mise à l'échelle selon l'axe X de 4)
b = 2 (mise à l'échelle selon l'axe X de 2)
alpha = 0 degrés (pas de rotation)m11 = a.cos(alpha) = 4.cos(0) = 4
m12 =b.sin(alpha) = 2.sin(0) = 0
m21 = a.(-sin(alpha)) = 4.(-sin(0)) = 0
m22 = b.cos(alpha) 2.cos(0) = 2Cet exemple montre que s'il n'y a pas de rotation, les facteurs d'échelle m11 et m22 valent respectivement a et b, c'est-à-dire qu'ils valent exactement le taux à appliquer, et m12 et m21 valent 0.
La procédure suivante permet de créer la matrice en passant les facteurs d'échelle, l'angle en degrés et les valeurs de translation.
Procedure.l GdipCreateMatrix2Ex(ScaleX.f, ScaleY.f, Angle.f, TranslateX.f, TranslateY.f) ; ScaleX --> facteur d'échelle voulu en X ; ScaleY --> facteur d'échelle voulu en Y ; Angle --> angle de rotation voulu en degrés ; TranslateX --> valeur de la translation voulue en X ; TranslateY --> valeur de la translation voulue en Y ; retourne 0 si la matrice n'a pas pu être initialisée ; sinon retourne l'ID système de la matrice Protected AngleRadian.f, *Localmatrix.l AngleRadian = #PI/180*Angle If GdipCreateMatrix2(ScaleX * Cos(AngleRadian), ScaleY * Sin(AngleRadian), ScaleX * (-Sin(AngleRadian)), ScaleY * Cos(AngleRadian), TranslateX, TranslateY, @*Localmatrix) = #Ok ProcedureReturn *Localmatrix Else ProcedureReturn 0 EndIf EndProcedure
Le fichier GdipCreateMatrix2_To_Rotate_Par_Angle30degres.pb utilise cette procédure et le résultat (rotation de 30 degrés d'un carré) correspond au même résultat que le fichier GdipRotateMatrix_30degres.pb qui utilise la fonction GdipRotateMatrix().
Les différents exemples suivants montrent comment agir individuellement sur chaque transformation.
Application à la mise à l'échelle :
Le fichier d'exemple GdipMultiplyMatrix_To_Scale.pb agit uniquement sur la mise à l'échelle, le résultat est équivalent à la fonction seule GdipScaleMatrix(). Le rendu est le même que pour le fichier d'exemple GdipScaleMatrix.pb mais avec des fonctions différentes.
Voici les codes des deux manières pour arriver au même résultat :
; Avec la fonction GdipMultiplyMatrix()
GdipCreateMatrix2(3, 0, 0, 2, 0, 0, @*matrix)
; application de la matrice au graphique
GdipSetWorldTransform(*gfx, *matrix.); Avec la fonction GdipScaleMatrix()
GdipCreateMatrix(@*matrix)
; Mise à l'échelle de la matrice
GdipScaleMatrix(*matrix, 3, 2, #MatrixOrderAppend)
; application de la matrice au graphique
GdipSetWorldTransform(*gfx, *matrix)A noter que pour la fonction GdipMultiplyMatrix(), tous les paramètres doivent être renseignés.
Il n'y a pas de rotation, m12 et m21 doivent être mis à 0.
Il n'y a pas de translation, dx et dy doivent être mis à 0.
Application à la rotation :
Le fichier d'exemple GdipMultiplyMatrix_To_Rotate.pb
agit uniquement sur la rotation, le résultat est équivalent
à la fonction seule GdipRotateMatrix().
Le rendu est le même que pour le fichier d'exemple GdipRotateMatrix.pb
mais avec des fonctions différentes.
rotation de 45 degrés.
Voici les codes des deux manières pour arriver au même résultat :; Avec la fonction GdipMultiplyMatrix()
AngleRadian.f = #PI/180*#Angle
GdipCreateMatrix2(Cos(AngleRadian), Sin(AngleRadian), -Sin(AngleRadian), Cos(AngleRadian), 0, 0, @*matrix)
; application de la matrice au graphique
GdipSetWorldTransform(*gfx, *matrix.)
; Avec la fonction GdipScaleMatrix()
; création de la matrice
GdipCreateMatrix(@*matrix)
; Rotation de 45 degrés
GdipRotateMatrix(*matrix, 45, #MatrixOrderAppend)
; application de la matrice au graphique
GdipSetWorldTransform(*gfx, *matrix)A noter que pour la fonction GdipMultiplyMatrix(), tous les paramètres doivent être renseignés.
Il n'y a pas de translation, dx et dy doivent être mis à 0.
Application à la translation :
Le fichier d'exemple GdipMultiplyMatrix_To_Translate.pb agit uniquement sur la translation (150 en X et 45 en Y), le résultat est équivalent à la fonction seule GdipTranslateMatrix(). Le rendu est le même que pour le fichier d'exemple GdipTranslateMatrix.pb mais avec des fonctions différentes.
Voici les codes des deux manières pour arriver au même résultat :; Avec la fonction GdipMultiplyMatrix()
GdipCreateMatrix2(1, 0, 0, 1, 150, 45, @*matrix)
; application de la matrice au graphique
GdipSetWorldTransform(*gfx, *matrix)
; Avec la fonction GdipRotateMatrix()
; création de la matrice
GdipCreateMatrix(@*matrix)
; Translation
GdipTranslateMatrix(*matrix, 150, 45, #MatrixOrderAppend)
; application de la matrice au graphique
GdipSetWorldTransform(*gfx, *matrix)A noter que pour la fonction GdipMultiplyMatrix(), tous les paramètres doivent être renseignés.
Il n'y a pas de mise à l'échelle, m11 et m22 doivent être mis à 1 (1 = 100% de la taille d'origine).
Il n'y a pas de rotation, m12 et m21 doivent être mis à 0.
Voir aussi le site sur
les transformations affines :
http://fr.wikipedia.org/wiki/Transformation_affine