Le paramètre order est important. Il défini l'ordre de la multiplication des matrices.
La multiplication des matrices n'est pas commutative. La multiplication de *matrix1 par *matrix2 est différente de la multiplication de *matrix2 par *matrix1.

L'origine du graphique est toujours le point X = 0 et Y = 0.

Exemple 1 :

Le premier exemple crée un graphique, dessine un carré en noir à X = 10, Y = 10, de 60 pixels de côté. On crée une matrice avec une translation en X de 150 et en Y de 45 pixels. Une rotation angulaire de 30 degrés dans le sens des aiguilles d'une montre est appliqué au graphique avec la fonction GdipRotateWorldTransform(). Puis on applique la matrice (donc la translation) au graphique. On dessine un carré en rouge aux mêmes coordonnées.

L'ordre des matrices étant important, voici comment se passe les choses avec les valeurs de l'exemple.

La première transformation appliquée au graphique est la rotation angulaire de 30 degrés, mais c'est le paramètre order qui défini si c'est cette transformation qui sera appliquée d'abord.
GdipRotateWorldTransform(*Localgfx, 30, #MatrixOrderPrepend)

Order vaut #MatrixOrderPrepend, ce qui signifie que cette opération (rotation) est appliquée avant la précédente opération si elle existe et comme il n'y en a pas, on applique de suite la rotation angulaire à l'ensemble du graphique. Ce paramètre n'a pas d'influence ici.
Tous les éléments affichés sur le graphique subiront cette transformation tant que l'on ne modifie pas la matrice du graphique qui est la résultante de toutes les transformations. Pour la rotation, le point de référence est le point X = 0 et Y = 0.

A ce moment, voilà ce que donne le dessin du carré avant rotation (en noir) puis après rotation de 30° (en rouge).

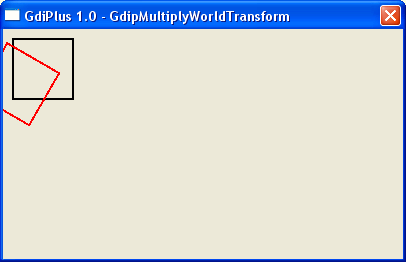
Ensuite on applique à tout le graphique la translation en X de 150 et en Y de 45 pixels avec la matrice et la fonction GdipMultiplyWorldTransform().

Order vaut #MatrixOrderAppend, ce qui signifie que cette opération (translation) est appliquée après la précédente opération si elle existe et c'est le cas, elle s'appliquera donc après la rotation angulaire.

Voilà ce que donne le dessin du carré avant rotation (en noir) puis après les deux transformations, rotation de 30° suivi de la translation (en rouge).

A noter que le paramètre order de la fonction GdipTranslateMatrix() ne s'applique qu'à la matrice qui n'a qu'une seule transformation, sa valeur peut indifféremment être #MatrixOrderPrepend ou #MatrixOrderAppend, cela n'aura pas d'influence.

Exemple 2:

Cet exemple est prsque identique au prmier sauf que le paramètre order de la fonction GdipMultiplyWorldTransform() vaut #MatrixOrderAppend.

Le second exemple crée un graphique, dessine un carré en noir à X = 10, Y = 10, de 60 pixels de côté. On crée une matrice avec une translation en X de 150 et en Y de 45 pixels. Une rotation angulaire de 30 degrés dans le sens des aiguilles d'une montre est appliqué au graphique avec la fonction GdipRotateWorldTransform(). Puis on applique la matrice (donc la translation) au graphique avec le paramètre order valant #MatrixOrderAppend. On dessine un carré en rouge aux mêmes coordonnées.

L'ordre des matrices étant important, voici comment se passe les choses avec les valeurs de l'exemple.

La première transformation appliquée au graphique est la rotation angulaire de 30 degrés, mais c'est le paramètre order qui défini si c'est cette transformation qui sera appliquée d'abord.
GdipRotateWorldTransform(*Localgfx, 30, #MatrixOrderPrepend)

Order vaut #MatrixOrderPrepend, ce qui signifie que cette opération (rotation) est appliquée avant la précédente opération si elle existe et comme il n'y en a pas, on applique de suite la rotation angulaire à l'ensemble du graphique. Ce paramètre n'a pas d'influence ici.

Ensuite on applique à tout le graphique la translation en X de 150 et en Y de 45 pixels avec la matrice et la fonction GdipMultiplyWorldTransform().

Order vaut #MatrixOrderPrepend, ce qui signifie que cette opération (translation) est appliquée avant la précédente opération si elle existe et c'est le cas, elle s'appliquera donc avant la rotation angulaire.

Tous les éléments affichés sur le graphique subiront d'abord une translation puis une rotation angulaire de 30 ° dans le sens des aiguilles d'une montre. Pour la rotation, le point de référence est le point X = 0 et Y = 0.

Pour décomposer, voilà ce que donne le dessin du carré avant les 2 transformations (en noir) puis après la translation (en bleu).

Voilà ce que donne le dessin du carré avant rotation (en noir) puis après les deux transformations, translation suivi de la rotation de 30° (en bleu).

A noter que le paramètre order de la fonction GdipTranslateMatrix() ne s'applique qu'à la matrice qui n'a qu'une seule transformation, sa valeur peut indifféremment être #MatrixOrderPrepend ou #MatrixOrderAppend, cela n'aura pas d'influence.

Voici réuni sur le même graphique ces deux exemples qui montrent bien l'importance du paramètre order des fonctions.