Le tracé inscrit à l'intérieur du rectangle défini par les points srcx.f, srcy.f, srcwidth.f et srcheight.f va subir une distorsion pour venir s'inscrire à l'intérieur du parallélogramme défini par le tableau de point destPoints.PointF. Le rendu final s'inscrit dans le parallélogramme si aucune matrice n'est appliquée.

Le parallélogramme peut être défini par 3 ou 4 points. Lorsqu'il est contient trois éléments, l'angle inférieur droit du parallélogramme est défini par les trois premiers points.

Correspondance entre les points du rectangle source et ceux du parallélogramme :

Parallélogramme défini par 3 points :

La transformation indiquée par un rectangle source et trois points de destination trace le contenu du rectangle dans un parallélogramme.

A l'angle supérieur gauche du rectangle correspond le point 0 du tableau destPoints.PointF
A l'angle supérieur droit du rectangle correspond le point 1 du tableau destPoints.PointF
A l'angle inférieur gauche du rectangle correspond le point 2 du tableau destPoints.PointF

Parallélogramme défini par 4 points :

La transformation indiquée par un rectangle source et quatre points de destination trace le contenu du rectangle dans un quadrilatère arbitraire qui n'est pas nécessairement un parallélogramme.

A l'angle supérieur gauche du rectangle correspond le point 0 du tableau destPoints.PointF
A l'angle supérieur droit du rectangle correspond le point 1 du tableau destPoints.PointF
A l'angle inférieur gauche du rectangle correspond le point 2 du tableau destPoints.PointF
A l'angle inférieur droit du rectangle correspond le point 3 du tableau destPoints.PointF

Le paramètre *matrix permet d'appliquer une matrice de transformation géométrique au tracé (mise à l'échelle, translation, rotation angulaire).

Le paramètre warpMode est une constante de l'énumération WarpMode qui définie le type de la distorsion, bilinéaire ou de perspective.

La fonction aplanie les courbes en fonction du paramètre flatness (voir les exemples de la fonction GdipFlattenPath().

Certaines fonctions ne stockent pas les points d'origine mais elles convertissent les courbes (spline cardinale etc.) en en une suite de courbes de Bézier et sauvegardent les points qui définissent ces courbes de Bézier. Un objet GraphicsPath stocke l'ensemble de ces points qui représentent des lignes et des courbes (converties ou non). Cette fonction de distorsion convertit ces points de sorte qu'ils ne représentent seulement que des lignes. Le paramètre de planéité (flatness) influence le nombre de lignes qui sont stockées. Les points d'origine qui représentent les courbes sont perdus.

Le premier fichier d'exemple dessine une suite de ligne en rouge qui représente le tracé d'origine. Le rectangle d'origine utilisée par la fonction GdipWarpPath() est dessiné en bleu et englobe le tracé d'origine. Le paramètre warpMode vaut #WarpModePerspective. On applique ensuite la distorsion avec aucune matrice et le paramètre flatness valant #FlatnessDefault. Le parallélogramme de destination est définit par 4 points et est dessiné en bleu. Le tracé modifié par la fonction est dessiné en noir.

Aperçu :

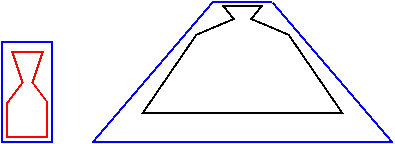
Le second fichier d'exemple est identique au premier sauf le paramètre warpMode qui vaut #WarpModeBilinear.

Aperçu :

Le troisième fichier d'exemple dessine un rectangle en rouge qui représente le tracé d'origine. Le paramètre warpMode vaut #WarpModePerspective. On définit une matrice qui appliquera un translation en x de 100 et de 0 en y. On applique la distorsion avec le paramètre flatness valant #FlatnessDefault. Le parallélogramme de destination est définit par 3 points et le tracé modifié par la fonction est dessiné en noir.

Le dernier fichier d'exemple est identique au troisième sauf le paramètre warpMode qui vaut #WarpModeBilinear.