Si la figure contient déjà une ou des lignes ou courbes et que l'on ne démarre pas une nouvelle figure, une ligne est ajoutée pour relier le point de terminaison du segment précédent au point de début de la courbe de Bézier.
Une courbe de Bézier cubique est définie par quatre points, la courbe passe par le premier et le dernier point (appelés noeuds) qui sont le point de départ et le point de terminaison (point d'arrivée). Les deux autres points sont des points de contrôle, ils permettent de définir la forme de la courbe, celle-ci ne passe pas par ces points de contrôle (sauf cas spéciaux avec noeuds alignés). Ces courbes sont très utilisées en dessin vectoriel, les points de contrôle correspondent aux "poignées" des objets utilisés en dessin vectoriel.
On pourrait comparer les deux points de commande à des aimants, ils attirent la courbe dans certaines directions en influençant sa courbure.
Les quatre points définissent l'enveloppe convexe de la courbe.
- Une courbe de Bézier est à l'intérieur de l'enveloppe convexe des points de contrôle.
- Une courbe de Bézier est un segment si et seulement si les points de contrôle sont alignés.
- Le contrôle de la courbe est global : modifier un point de contrôle modifie toute la courbe et non pas le voisinage du point de contrôle.
Exemples de courbes :
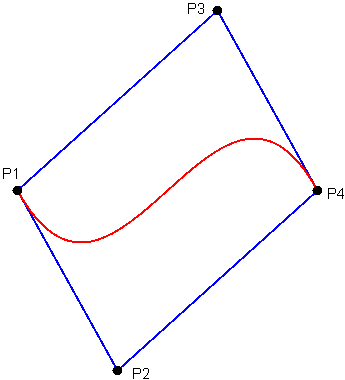
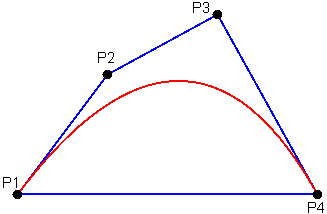
La courbe est en rouge et l'enveloppe en bleu.
P1 est le point de départ.
P2 et P3 sont les points de contrôle.
P4 est le point final.
Entre les 2 courbes, seul le point P2 (point de contrôle) n'a pas les
mêmes coordonnées.
La courbe de Bézier est fortement modifiée.